Day2

# MySQL三层B+树能存多少数据？

具体答案题解很详细，这里只补充下思路及扩展知识点。

# 答题思路

一般这种题，更多的是考察对于MySQL存储格式的了解，后续遇到类似的面试题该如何思考？接下来按步骤分析以下。

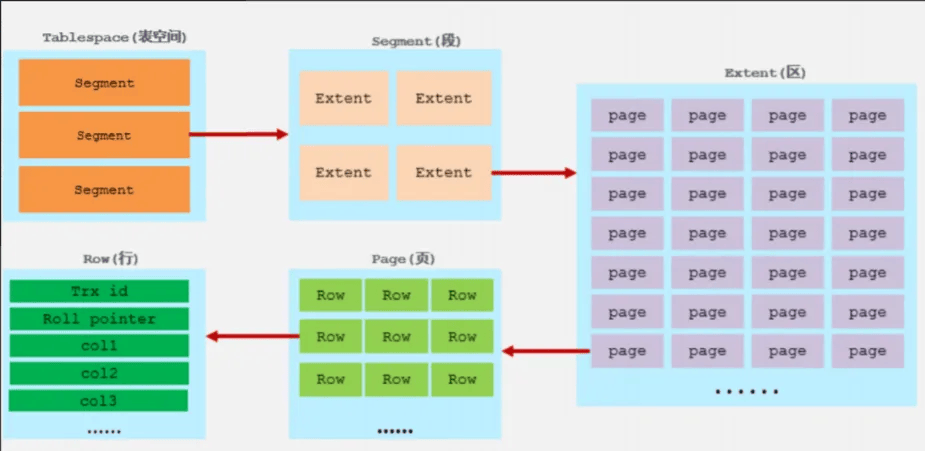
1. 了解MySQL的存储格式及对应的结构（如每页默认大小16KB，B+树的结构）
2. 假设数据大小，估算每页可存储数据数量
3. 假设索引键和指针大小，估算单个节点的扇出数量
4. 通过（单页存储数据量×单个节点的扇出量2 ）计算总数据量，这里三层就是2次方，n层就是n-1次方。

# 扩展知识（了解即可）

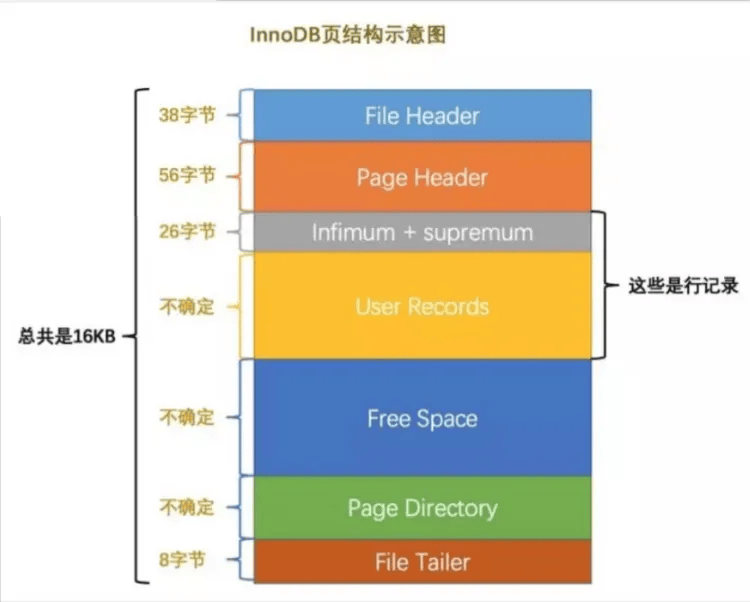
# InnoDB的存储格式

# 页结构

# 引导思路及假想面试

Q ：上面问题回答的不错，那你是否了解B+树的存储结构呢？

A :

1. B+树是一棵平衡树，每个叶子节点到根节点的路径长度相同，查询效率高
2. B+树的所有关键字都在叶子节点上，因此范围查询时只需要遍历一遍叶子节点即可；
3. B+树的叶子节点都按照关键字大小顺序存放，因此可以快速地支持按照关键字大小进行排序
4. B+树的非叶子节点不存储实际数据，因此可以存储更多的索引数据
5. B+树的非叶子节点使用指针链接子节点，因此可以快速地支持范围查询和倒序查询
6. B+树的叶子节点之间通过双向链表链接，方便进行范围查询

Q : 你是否了解与B+树类似的数据结构？

A ：

• 红黑树：红黑树是一种自平衡的二叉查找树，是在普通二叉查找树的基础上，通过对节点进行红黑着色以及一些特定的旋转操作来保持树的平衡，从而保证高效的查找、插入和删除操作。
• B树：B 树是一种平衡的多路查找树，它允许每个节点包含多个关键字和对应多个子树，能够有效地减少磁盘 I/O 操作次数，提高查找效率，适用于外存（如磁盘）数据的存储和检索。

Q : 那为什么不选择红黑树或者B树呢？

A：因为B+树只有叶子节点存储数据，非叶子节点不存储数据且节点大小固定。还有就是叶子节点之间通过双向链表链接，所以B+树实现索引有很多优势，比如上面提到的范围查询、可以存储更多的索引数据、有利于优化排序等，这些红黑树和B树是做不到的

# MySQL的最左前缀匹配原则是什么？

# 简要回答

最左前缀匹配是指在查询中利用索引的最左边的部分进行匹配。假设有一个联合索引idx_c1_c2_c3（c1,c2,c3），查询条件针对c1、（c1,c2）、（c1,c2,c3）例如 where c1 ='xxx' and c2 ='xxx' 都可以利用这个联合索引进行最左前缀匹配。

如果用的是（c1,c3）也是可以走索引的，只不过用到是c1这个字段的索引。

在不考虑跳跃扫描等其他优化的情况下，如果查询条件只涉及到c2 、c3、（c2,c3）等不包含c1的话，如此就是没有遵守最左前缀匹配，所以也就不能利用这个索引进行最左前缀匹配。

# 补充回答

• 最左前缀匹配和查询条件的顺序没有关系，比如查询条件为 where c1 ='xxx' and c2 ='xxx'或者 where c2 ='xxx' and c1 ='xxx'，对结果没有影响，同样会命中索引。
• 如果不涉及联合索引，单个字段的索引也需要遵守最左前缀，假设有一个字段值为'abc'时，当我们使用like进行模糊匹配时，like'%ab'可以走索引，而其余情况如'%bc'、'b%c'等都是不行的。
• 创建一个组合索引（c1,c2,c3），数据库会创建一个B+树，只不过在这棵树中，是先按照c1排序，c1相同时再按照c2排序，c2相同再按照c3排序，依次类推。同时也是上述也是B+树的查询原理。

详细看下图解释，假设有一个T1表数据如下

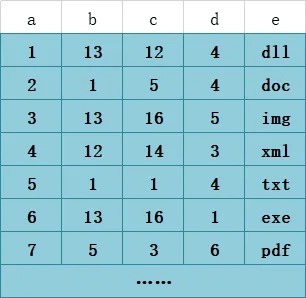
创建一个联合索引(b,c,d),构建B+树索引如下

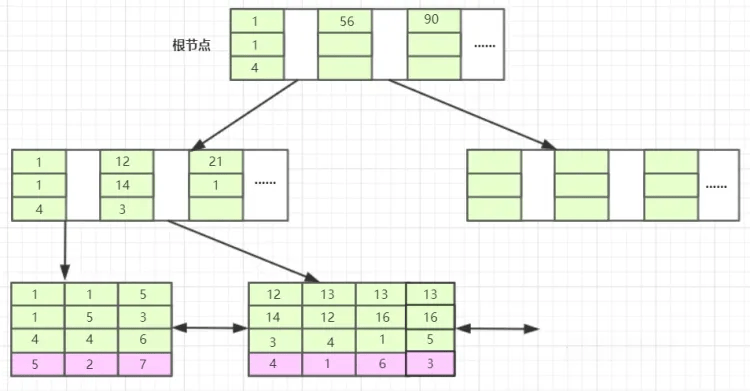
黄色部分为联合索引，紫色部分为主键值。黄色部分由上至下分别为b,c,d列值，由图可以看出排序也是先通过b列值大小排序后，如果相等再按照c列值排序，依次进行排序。

# 扩展回答

• Q：既然了解了最左匹配前缀原则，那为什么要遵循最左前缀匹配呢?
• A:

因为索引底层是一个B+树，如果是联合索引的话，在构造B+树的时候，会先按照左边的Key进行排序，左边的key相同时再一次按照右边的Key排序，所以再通过索引查询的时候，需要遵守最左前缀匹配原则，也就是需要从联合索引的最左边开始进行匹配。

• Q： 如果使用了联合索引，执行计划中key也有值还是很慢怎么办？
• A：

一般key有值并且type=index的情况很多人认为是走了索引的，但是当我们通过执行计划查看一个SQL的执行过程时，通常会遇见以下这种执行计划

+----+-------+---------------+----------+--------------------------+                                           
| id | type  | possible_keys | key      | Extra                    |                                           
+----+-------+---------------+----------+--------------------------+                                           
|  1 | index | NULL          | idx_abcd | Using where; Using index |                                           
+----+-------+---------------+----------+--------------------------+ 

上面可以看到Extra中的内容应该是Using index 而不是Using where; Using index 。所以根据这个执行计划可以了解到，SQL确实用到了idx_abcd的索引树，但是并没有直接通过索引进行匹配或者范围查询，而是扫描了整个索引树。所以type=index意味着全索引扫描，比扫表快一些，但和通常意义上理解的走索引不是一个概念，因此这种情况，大概率因为没有遵守最左前缀匹配导致的索引失效，所以需要调查查询语句或者修改索引来解决。

# 为什么MySQL选择使用B+树作为索引结构？

# 简要回答

• 支持范围查询，B+树在进行范围查找时，只需要从根节点一直遍历到叶子节点，因为数据都存储在叶子节点上，而且叶子节点之间有指针连接，可以很方便地进行范围查找。
• 支持排序，B+树的叶子节点按照关键字顺序存储，可以快速支持排序操作，提高排序效率；
• 存储更多的索引数据，因为它的非叶子节点只存储索引关键字，不存储实际数据，因此可以存储更多的索引数据；
• 在节点分裂和合并时，IO操作少。B+树的叶子节点的大小是固定的，而且节点的大小一般都会设置为一页的大小，这就使得节点分裂和合并时，IO操作很少，只需读取和写入一页。
• 有利于磁盘预读。由于B+树的节点大小是固定的，因此可以很好地利用磁盘预读特性，一次性读取多个节点到内存中，这样可以减少IO操作次数，提高查询效率。
• 有利于缓存。B+树的非叶子节点只存储指向子节点的指针，而不存储数据，这样可以使得缓存能够容纳更多的索引数据，从而提高缓存的命中率，加快查询速度。

# 补充回答

红黑树、B树、B+树的区别

比较项目	红黑树	B 树	B + 树
定义	一种自平衡的二叉查找树，通过红黑着色和旋转操作保持平衡	一种平衡的多路查找树，允许每个节点包含多个关键字和多个子树	B 树的变形，所有数据存储在叶子节点，叶子节点间有链表相连
节点结构	每个节点包含一个关键字、两个子节点指针以及颜色属性	每个节点包含多个关键字和多个子节点指针	非叶子节点只存储索引，叶子节点存储所有数据及链表指针
树的高度	较高，为 O (log n)，n 为节点数	相对较低，与节点能容纳的关键字数量有关	相对 B 树更低，同样依赖于节点容纳的关键字数量
查找效率	O (log n)，适用于内存中数据的快速查找	减少磁盘 I/O 次数	在范围查找上更高效
插入删除操作	插入和删除后需要通过旋转和重新着色来保持平衡，操作相对复杂	插入可能导致节点分裂，删除可能导致节点合并，操作涉及节点调整	类似 B 树，但可能需要额外调整叶子节点的链表
数据存储位置	数据存储在每个节点中	数据存储在每个节点中	所有数据存储在叶子节点
应用场景	常用于内存中的数据集合，如 Java 的 TreeMap、C++ 的 map 等	文件系统和数据库系统中，用于存储索引数据	数据库系统的索引结构，如 MySQL 的 InnoDB 存储引擎